Hồi quy để xác định cụ thể trọng số của từng nhân tố độc lập tác động đến nhân tố phụ thuộc như thế nào. Bài viết dưới đây là giúp bạn đọc hiểu được tại sao hồi quy lại quan trọng trong phân tích thông qua tìm hiểu cách chạy hồi quy SPSS cùng với hướng dẫn cách đọc kết quả hồi quy, tra ý nghĩa chỉ số chuẩn chỉnh và đánh giá các giả định thông qua biểu đồ.
1. Hồi quy tuyến tính SPSS là gì?
Hồi quy SPSS là một phương pháp sử dụng để đánh giá độ bền của mối quan hệ giữa các biến phụ thuộc và độc lập. Nó giúp dự đoán giá trị của một biến phụ thuộc từ một hoặc nhiều biến độc lập cũng như giúp dự đoán có bao nhiêu phương sai được tính trong một phản hồi (biến phụ thuộc) bởi một tập hợp các biến độc lập.

2. Cách chạy hồi quy tuyến tính trong SPSS
Để hiểu rõ hơn về cách chạy hồi quy tuyến tính trong SPSS, chúng ta sẽ đến với ví dụ cụ thể dưới đây:
2.1. Giả định hồi quy
Khi phân tích dữ liệu bằng cách sử dụng hồi quy SPSS, một phần quan trọng để đảm bảo rằng dữ liệu phân tích thực sự có thể được phân tích bằng cách sử dụng hồi quy tức có nghĩa là phải “vượt qua” bảy giả định cần thiết cho hồi quy tuyến tính để cung cấp một kết quả hợp lệ.
- Giả định số 1: Biến phụ thuộc phải được đo lường ở mức liên tục (tức là, nó là một biến khoảng hoặc biến tỷ lệ).
- Giả định số 2: Biến độc lập của bạn cũng nên được đo lường ở mức liên tục (tức là, nó là một biến khoảng hoặc biến tỷ lệ).
- Giả thiết số 3: Cần có một mối quan hệ tuyến tính giữa hai biến.
- Giả định số 4: Không có giá trị ngoại lệ đáng kể nào.
- Giả định số 5: Nên có sự độc lập của các quan sát, có thể dễ dàng kiểm tra bằng cách sử dụng thống kê Durbin-Watson.
- Giả định số 6: Dữ liệu cần phải thể hiện tính đồng biến.
- Giả định số 7: Cuối cùng, cần kiểm tra xem phần dư (lỗi) của đường hồi quy có được phân phối gần đúng chuẩn hay không.
Lưu ý:
– Không phải lúc nào cũng ra kết quả đẹp nhất, đôi khi phân tích dữ liệu bằng thống kê SPSS, một hoặc nhiều giả định này bị vi phạm (tức là không được đáp ứng).
– Các giả định số 3 nên được kiểm tra trước tiên, trước khi chuyển sang kiểm tra các giả định số 4, 5, 6 và 7.
2.2. 5 bước chạy hồi quy SPSS
Đặt vấn đề: Một nhân viên bán hàng cho một thương hiệu xe hơi lớn muốn xác định liệu có mối quan hệ giữa thu nhập của một cá nhân và giá họ phải trả cho một chiếc xe hơi hay không. Như vậy, “thu nhập” của cá nhân là biến độc lập và “giá” mà họ phải trả cho một chiếc ô tô là biến phụ thuộc.
Thiết lập thống kê:
- Trong SPSS, chúng ta sẽ tạo hai biến để có thể nhập dữ liệu của: Thu nhập (biến độc lập) và Giá (biến phụ thuộc).
- Có thể tạo một biến thứ ba caseno để hoạt động như một số trường hợp theo thứ tự thời gian. Biến thứ ba này được sử dụng để giúp dễ dàng loại bỏ các trường hợp như ngoại lệ quan trọng mà bạn đã xác định khi kiểm tra các giả định.
Chạy thống kê: Năm bước dưới đây hướng dẫn cho bạn phân tích dữ liệu bằng cách sử dụng hồi quy trong SPSS khi không có giả định nào trong bảy giả định trong phần trước bị vi phạm. 5 bước chạy mô hình hồi quy trong SPSS như sau:
- Bước 1: Trên thanh công cụ, nhấp chọn: Analyze – Regression – Linear.
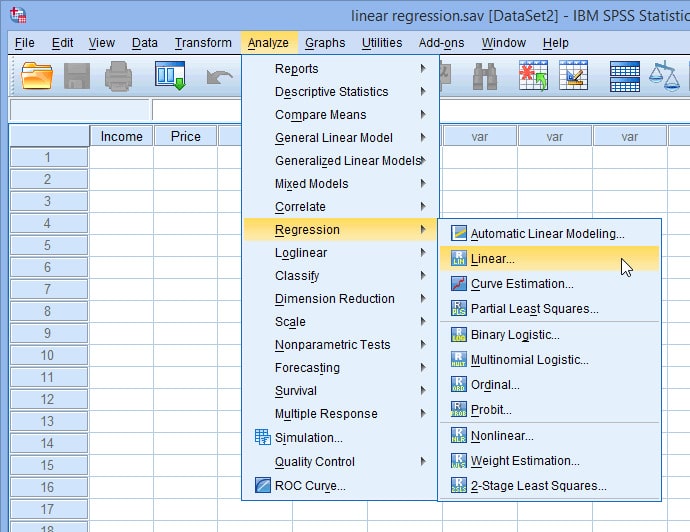
- Bước 2: Kéo thả biến phụ thuộc “thu nhập” vào ô Independent(s) và chuyển biến độc lập “giá” vào ô Dependent.
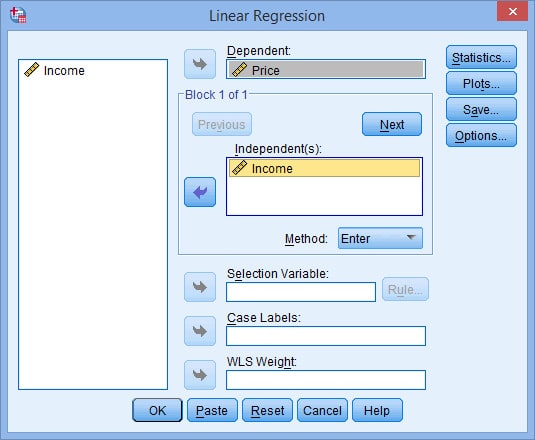
- Bước 3: Bấm vào ô Statistics, sau đó cửa sổ “Linear Regression: Statistics” mở ra rồi chọn Collinearity diagnostics (để tính ra hệ số VIF – hệ số phóng đại phương sai) để đánh giá hiện tượng đa cộng tuyến. Sau đó nhấn vào ô Continue để trở lại hộp thoại Linear Regression.
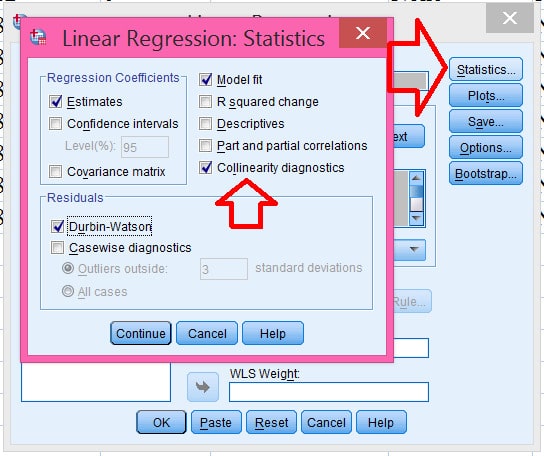
Qua bước 3 thì bốn trong số bảy giả định đã đề cập ở trên không bị vi phạm: Không có ngoại lệ đáng kể (giả định số 3), tính độc lập của các quan sát (giả định số 4), đồng biến đổi dạng (giả định số 5), và phân phối chuẩn của sai số/phần dư (giả định số 6).
- Bước 4: Nhấn OK để kết thúc.
- Bước 5: Diễn giải và nhận xét kết quả chạy hồi quy tuyến tính trong SPSS.
3. Đọc kết quả hồi quy trong SPSS
SPSS sẽ xuất ra rất nhiều bảng kết quả đầu ra, nhưng chúng ta cần tập trung sử dụng 3 bảng trọng tâm để phục vụ bài nghiên cứu.
3.1. Bảng ANOVA
Bảng ANOVA thể hiện báo cáo mức độ phù hợp của phương trình hồi quy với dữ liệu (tức là dự đoán biến phụ thuộc).
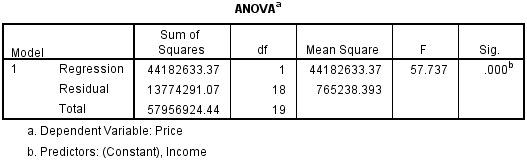
Trong ví dụ, bảng ANOVA chỉ ra rằng mô hình hồi quy dự đoán biến phụ thuộc tốt một cách đáng kể. Bởi vì hàng Hồi quy và cột Sig cho thấy ý nghĩa thống kê của mô hình hồi quy đã được chạy. Ở đây, p <0,0005, nhỏ hơn 0,05, và chỉ ra rằng về tổng thể, mô hình hồi quy dự đoán có ý nghĩa thống kê về biến kết quả (tức là nó phù hợp với dữ liệu).
3.2. Bảng Model Summary
Bảng Model Summary cung cấp các giá trị R và R 2. Trong ví dụ trên, bảng ANOVA thể hiện:
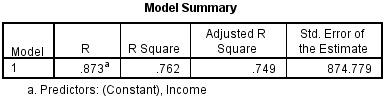
- Giá trị R đại diện cho mối tương quan đơn giản và là 0,873 (Cột R), cho biết mức độ tương quan cao.
- Giá trị R 2 (cột R Square) cho biết có bao nhiêu phần trăm trong tổng số thay đổi trong biến phụ thuộc “giá” có thể được giải thích bằng biến độc lập “thu nhập” . Trong trường hợp này, 76,2% có thể được giải thích, một con số rất lớn.
3.3. Bảng Coefficients
Bảng Coefficients cung cấp cho chúng ta thông tin cần thiết để dự đoán giá từ thu nhập, cũng như xác định xem thu nhập có đóng góp đáng kể về mặt thống kê vào mô hình hay không (bằng cách xem cột ” Sig. “).
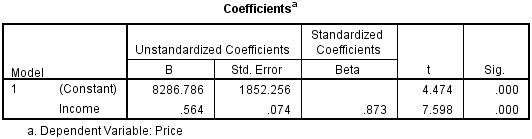
Hơn nữa, chúng ta có thể sử dụng các giá trị trong cột ” B ” trong cột ” Hệ số không chuẩn hóa “, như được hiển thị bên dưới để trình bày phương trình hồi quy dưới dạng:
Giá = 8287 + 0,564 (Thu nhập)
4. Ý nghĩa chỉ số trong hồi quy SPSS
5 chỉ số trong hồi quy SPSS có ý nghĩa như sau:
Giá trị Adjusted R Square (R bình phương hiệu chỉnh) và R2 (R Square)
Hai giá trị này cho biết mức độ ảnh hưởng của các biến độc lập lên biến phụ thuộc. Mức biến thiên của R và R2 là từ 0 – 1. Nếu nằm trong khoảng từ 0.5 – 1 thì là mô hình tốt, ngược lại nếu < 0.5 là mô hình chưa tốt. Càng tiến về 1 thì mô hình càng có ý nghĩa và ngược lại nếu càng tiến về 0 tức là ý nghĩa mô hình càng yếu.
Trị số Durbin – Watson (DW)
Chỉ số DW có chức năng kiểm tra hiện tượng tự tương quan bậc nhất. Giá trị của DW biến thiên dao động trong khoảng từ 0 đến 4:
- Nếu tương quan của các sai số liền kề nhau không xảy ra thì giá trị sẽ gần bằng 2.
- Nếu giá trị gần về 4 thì các phần sai số có tương quan nghịch, gần về 0 thì các phần sai số có tương quan thuận.
- Trong trường hợp DW < 1 và DW > 3 thì xảy ra hiện tượng tự tương quan chuỗi bậc nhất.

Giá trị Sig của kiểm định F
Giá trị Sig của F có tác dụng kiểm định độ phù hợp của mô hình hồi quy. Ở bảng kết quả ANOVA, nếu giá trị Sig. < 0.05 thì có thể suy ra rằng: Mô hình hồi quy tuyến tính bội và tập dữ liệu phù hợp và ngược lại.
Giá trị Sig của kiểm định t
Giá trị Sig của T được sử dụng để kiểm định ý nghĩa của hệ số hồi quy. Nếu Sig. <0.05 thì kết luận rằng: Biến độc lập có tác động đến biến phụ thuộc.
Hệ số phóng đại phương sai VIF (Variance inflation factor)
Hệ số VIF dùng để kiểm tra hiện tượng đa cộng tuyến.
- Nếu VIF > 10 thì có hiện tượng đa cộng tuyến xảy ra với biến độc lập đó. Khi đó, biến này sẽ không có giá trị giải thích biến thiên của biến phụ thuộc trong mô hình hồi quy.
- Nếu VIF < 2 thì không có hiện tượng đa cộng tuyến giữa các biến độc lập và ngược lại.
5. Đánh giá giả định hồi quy qua 3 biểu đồ
Chúng ta có thế đánh giá các giả định hồi quy theo 3 kiểu biểu đồ như sau.
5.1. Biểu đồ tần số phần dư chuẩn hóa Histogram
Đối với biểu đồ Histogram, nếu giá trị trung bình Mean gần bằng 0, độ lệch chuẩn gần bằng 1, đường cong phân phối có dạng hình chuông thì chúng ta đủ lập luận để khẳng định phân phối là xấp xỉ chuẩn, giả định phân phối chuẩn của phần dư không bị vi phạm.
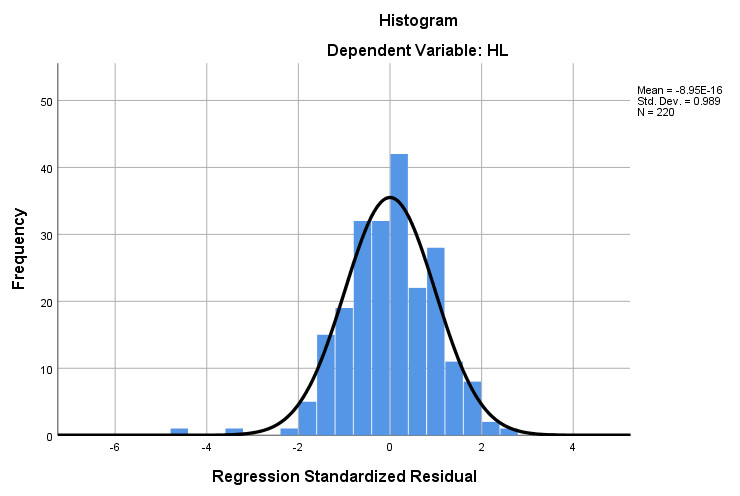
Từ biểu đồ chúng ta có thể thấy rằng:
- Có một đường cong phân phối chuẩn được đặt xếp chồng lên biểu đồ tần số. Đường cong có dạng hình chuông hoặc parabol, phù hợp với dạng đồ thị của phân phối chuẩn.
- Giá trị trung bình Mean = -8.95E-16 gần bằng 0, độ lệch chuẩn là 0.989 gần bằng 1, như vậy có thể nói, phân phối phần dư xấp xỉ chuẩn.
Kết luận: Giả thiết phân phối chuẩn của phần dư không bị vi phạm.
5.2. Biểu đồ phần dư chuẩn hóa Normal P-P Plot
Biểu đồ P-P Plot cũng là một dạng biểu đồ được sử dụng phổ biến nhằm giúp nhận diện sự vi phạm giả định phần dư chuẩn hóa.
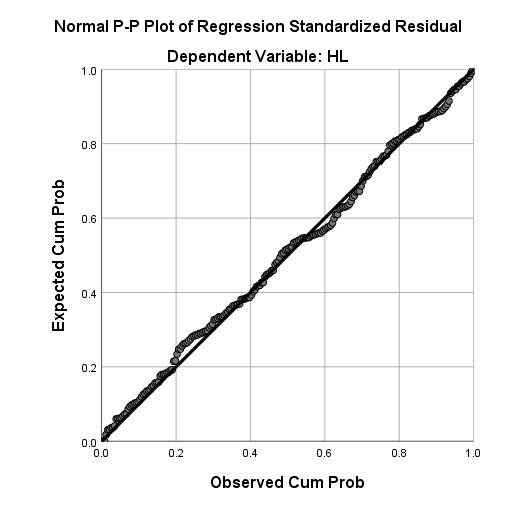
Đối với biểu đồ Normal P-P Plot, nếu các điểm phân vị trong phân phối của phần dư tập trung thành 1 đường chéo, nghĩa là phần dư có phân phối chuẩn và giả định phân phối chuẩn của phần dư không bị vi phạm.
Theo như ví dụ minh họa, các điểm phân vị trong phân phối của phần dư tập trung thành một đường chéo, từ đó suy ra giả định phân phối chuẩn của phần dư không bị vi phạm.
5.3. Biểu đồ Scatter Plot kiểm tra giả định liên hệ tuyến tính
Biểu đồ phân tán Scatter Plot giữa các phần dư chuẩn hóa và giá trị dự đoán chuẩn hóa giúp dò tìm xem dữ liệu hiện tại có vi phạm giả định liên hệ tuyến tính hay không.
Nếu phần dư chuẩn hóa phân bổ ngẫu nhiên xung quanh đường tung độ 0 và hình dạng tạo thành một đường thẳng thì có thể kết luận giả định quan hệ tuyến tính không bị vi phạm.
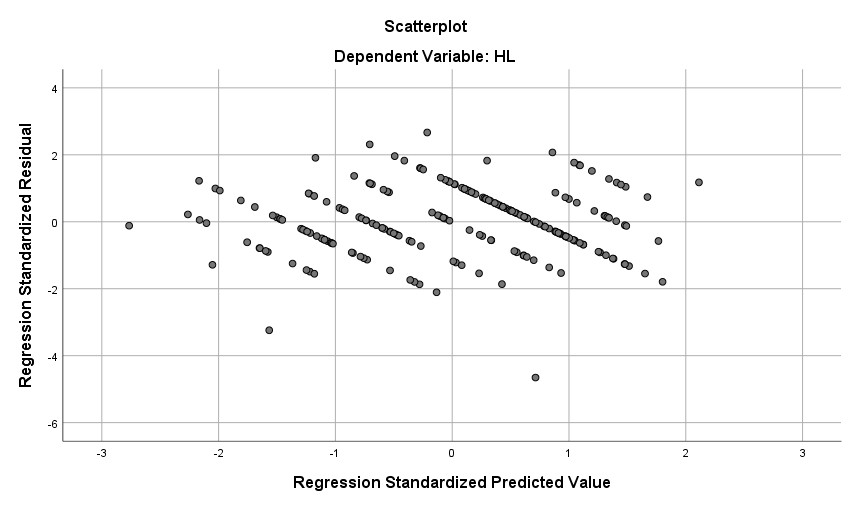
Trong ví dụ minh họa, phần dư chuẩn hóa phân bổ ngẫu nhiên tập trung xung quanh đường tung độ 0 tạo thành dạng đường thẳng, do đó có thể khẳng định giả định quan hệ tuyến tính giữa biến phụ thuộc với các biến độc lập không bị vi phạm.
Như vậy, bài viết đã mang đến cho bạn đọc thông tin chi tiết về cách chạy hồi quy trong SPSS và thông tin liên quan đến hồi quy. Qua đây mong rằng bạn đọc sẽ có thêm tài liệu nghiên cứu để áp dụng cho bài nghiên cứu khoa học của mình. Chúc các bạn thành công!











