Mô hình ARIMA đã không còn xa lạ đối với sinh viên – học viên chuyên ngành kinh tế với ứng dụng thực tiễn quan trọng trong kinh tế lượng đặc biệt là lĩnh vực tài chính, chứng khoán. Vậy mô hình ARIMA là gì? Cách chạy mô hình ARIMA trên Eviews thế nào cho chuẩn? Tất cả những thắc mắc trên sẽ được Best4Team giải đáp ngay trong bài viết thú vị dưới đây. Xem ngay bạn nhé!
1. Mô hình ARIMA trên Eviews là gì?
Trước khi tìm hiểu cách chạy mô hình ARIMA trên Eviews thì trước tiên chúng ta cần làm rõ khái niệm mô hình này.
- Mô hình ARIMA là viết tắt của cụm từ Autoregressive Integrated Moving Average và là một trong những kỹ thuật phổ biến và được sử dụng rộng rãi nhất để dự báo chuỗi thời gian đơn biến.
- Một số biến số bạn có thể dự báo bằng mô hình ARIMA là: GDP, Chỉ số giá tiêu dùng (CPI) và giá cổ phiếu hoặc hàng hóa
2. Cấu hình mô hình ARIMA
Mô hình ARIMA được giới thiệu lần đầu tiên vào năm 1976 bởi 2 nhà kinh tế Box và Jenkins. Cấu hình của mô hình ARIMA gồm có 3 phần:
- Phần AR hay Autoregressive (tự hồi quy), lấy giá trị q: Cho thấy rằng biến quan tâm đang phát triển được hồi quy trên những giá trị trước đó của chính nó.
- Phần I ký hiệu của Integrated (chuỗi ổn định sau khi chuyển sang dạng sai phân), lấy giá trị d: Chỉ rõ các giá trị dữ liệu đã được thay thế bằng sự chênh lệch giữa các giá trị mà nó thể hiện so với các giá trị trước đó của chính nó.
- Phần MA hay Moving average (bình quân di động), lấy giá trị p: Cho thấy lỗi hồi quy là tổ hợp tuyến tính của các thuật ngữ bị lỗi có giá trị xảy ra đồng thời với nhau và tại những thời điểm khác nhau ở trong quá khứ.
3. Phần mềm dự báo ARIMA
Mô hình ARIMA dự báo chuỗi thời gian được tích hợp trên nhiều phần mềm, điển hình với 4 phần mềm tiêu biểu:
- Mô hình dự báo ARIMA trong phần mềm SPSS
- Mô hình dự báo ARIMA trong R
- Mô hình ARIMA dự báo kinh tế trong STATA
- Mô hình ARIMA trên Eviews
Trong số các mô hình kể trên, mô hình ARIMA trên phần mềm Eviews được xem là mô hình dự báo được sử dụng phổ biến nhất hiện nay và đem lại hiệu quả cao.
4. Phương pháp Jenkins là gì?
Trong cách chạy mô hình ARIMA trên Eviews, phương pháp phổ biến nhất là phương pháp Box Jenkins được đặt theo tên của 2 tác giả George Box và Gwilym Jenkins. Phương pháp này gồm 4 giai đoạn:
- Giai đoạn xác nhận mô hình thực nghiệm
- Giai đoạn ước lượng mô hình ARIMA
- Giai đoạn kiểm định mô ARIMA hình bằng chẩn đoán
- Giai đoạn dự báo bằng mô hình ARIMA
4.1. Giai đoạn xác nhận mô hình thực nghiệm
Ví dụ: Áp dụng cách chạy mô hình mô hình ARIMA trên Eviews nhằm điều chỉnh mô hình ARIMA cho loạt bài “chỉ số giá tiêu dùng – Hoa Kỳ ”.
Tổng quan về Box Jenkins:
- ARIMA được viết là ARIMA (p, d, q), trong đó:
- “p” là thứ tự của thành phần tự động hồi phục
- “d” là thời gian chúng ta cần phân biệt biến để đạt được tính ổn định
- “q” là thứ tự của chuyển động phần tử trung bình.
- Công thức tính:
Trong đó:
- c = Thứ tự không đổi
- p = Thứ tự thành phần tự hồi quy
- q = Hệ số thành phần trung bình
- α = Hệ số thành phần tự hồi quy của mô hình
- θ = Trung bình động
- Et = Lỗi thuật ngữ
- Giai đoạn xác nhận mô hình thực nghiệm, chúng ta sẽ xác định “p”, “d” và “q” và tập trung vào 2 khía cạnh:
- Kiểm tra tính ổn định của biến quan tâm.
- Xác định thứ tự của các thành phần tự động hồi quy và trung bình động.
Kiểm tra sự cố định:
Để kiểm tra tính ổn định của biến quan tâm, chúng ta xem xét 3 yếu tố:
- Đồ thị
- Đồ thị tương quan
- Kiểm tra chính thức: Tăng cường Dickey Fuller, Kiểm tra Phillips-Perron và kiểm tra KPSS.
Cách xác định thứ tự của “p” và “q”:
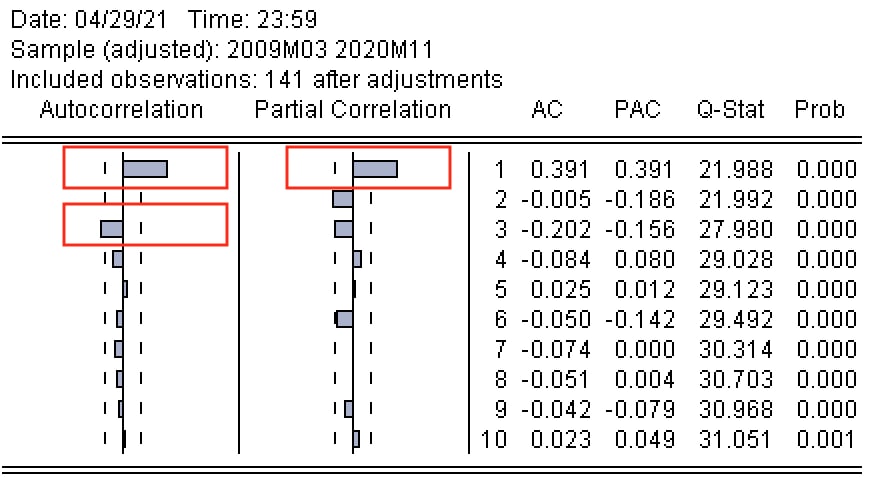
Để xác định thứ tự của các thành phần tự hồi quy và trung bình động hay tìm cách xác định pdq trong mô hình ARIMA, chúng ta sẽ tập trung vào tương quan của “CPI” trong những khác biệt đầu tiên.
- Để xác định thứ tự của thành phần tự tương quan (“p”), chúng ta phải quan sát cột Tự tương quan từng phần (PACF).
=> Chúng ta quan sát thấy một dải tin cậy ở các bên. Các giá trị vượt quá dải cho thấy thứ tự có thể có của thành phần tự động khôi phục.
=> Nhìn vào biểu đồ tương quan, độ trễ đầu tiên là một thành phần AR (1) rất quan trọng, sau đó độ trễ 2 và 3 đang ở trên mạng và có thể được kiểm tra
- Để xác định thứ tự của thành phần trung bình động (“q”), chúng ta phải quan sát cột Tự tương quan (ACF).
=> Chúng ta có thể thấy rằng độ trễ 1 và 3 vượt quá dải tin cậy
=> Do đó, có thể có hai thành phần trung bình động MA (1) và MA (3).
- Lưu ý: Bạn cũng có thể thử lắp nhiều thành phần AR hơn. Đối với ví dụ này, chúng ta sẽ bám vào các mô hình khả thi đã chọn: ARIMA (1,1,1) và ARIMA (1,1,3).
4.2. Giai đoạn ước lượng mô hình ARIMA
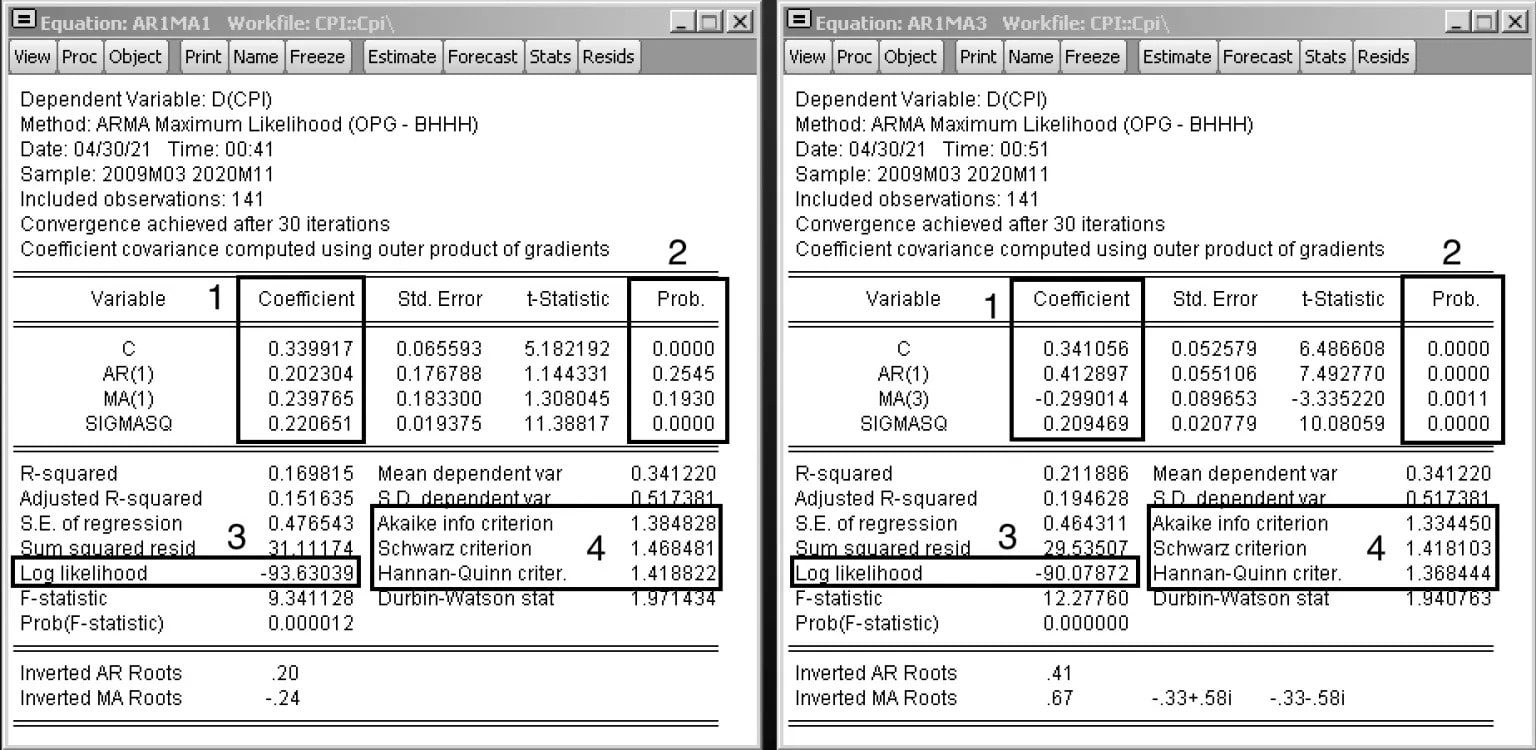
Khi đã xác định được các ứng cử viên mô hình ARIMA có thể có, bạn cần ước tính chúng và quyết định mô hình nào là thích hợp nhất. Hai mô hình quyết định ước tính trong ví dụ gồm có:
- ARIMA (1,1,1)
- ARIMA (1,1,3)
Các bước thực hiện:
Trong phương pháp Box Jenkins về cách chạy mô hình ARIMA trên Eviews, ở giai đoạn ước lượng mô hình ARIMA, bạn cần thực hiện 4 công việc sau:
- Ước tính các mô hình ARIMA đã xác định trong Giai đoạn 1.
- Chọn một mô hình dựa trên tầm quan trọng của các ước tính hệ số.
- Chọn một mô hình dựa trên các tiêu chí mô hình: Schwartz, Akaike và Hannan-Quinn.
- Mô hình có giá trị nhỏ nhất trong các tiêu chí của mô hình. Hệ số có ý nghĩa nhất sẽ là mô hình thích hợp nhất.
Cách chạy mô hình ARIMA trên Eviews để ước lượng:
Có 2 cách để thực hiện, gồm có:
-
- Cách 1: Chọn chức năng Proc > Automatic ARIMA Forecasting
- Cách 2: Sử dụng câu lệnh ls d(cpi) c ar(1) ma(1) và ls d(cpi) c ar(1) ma(3)
Cách chọn mô hình ARIMA thích hợp nhất:
- Để chọn mô hình thích hợp nhất, bạn nên lập bảng và điền thông tin với dữ liệu thu được trong hình bên trên (mô hình ARIMA ước tính):
- Khi chọn mô hình ARIMA thích hợp nhất, bạn cần đảm bảo 4 điều kiện sau:
- Mức độ quan trọng của các điều khoản ARMA: chọn mô hình có các điều khoản quan trọng nhất (giá trị p <0,05).
- SigmaSQ: là thước đo độ biến động. Chọn cái nhỏ nhất.
- Khả năng ghi nhật ký: Chúng tôi cần chọn giá trị lớn nhất, vì chúng tôi đang tối đa hóa hàm khả năng ghi nhật ký (giá trị lớn nhất là giá trị âm nhỏ nhất).
- Tiêu chí lựa chọn mô hình: Chọn mô hình có Akaike, Schwarz và Hannan-Quinn nhỏ nhất.
Kết luận:
Mô hình ARIMA (1,1,3) phù hợp hơn mô hình ARIMA (1,1,1)
4.3. Giai đoạn kiểm định mô hình bằng chẩn đoán
Điều kiện kiểm định mô hình bằng chẩn đoán:
Kiểm định mô hình bằng chẩn đoán là giai đoạn thứ 3 trong cách chạy mô hình ARIMA trên Eviews. Ở giai đoạn này, bạn cần đảm bảo 2 điều kiện sau:
- Không xảy ra tự tương quan
- Đảm bảo mô hình đáp ứng các điều kiện ổn định
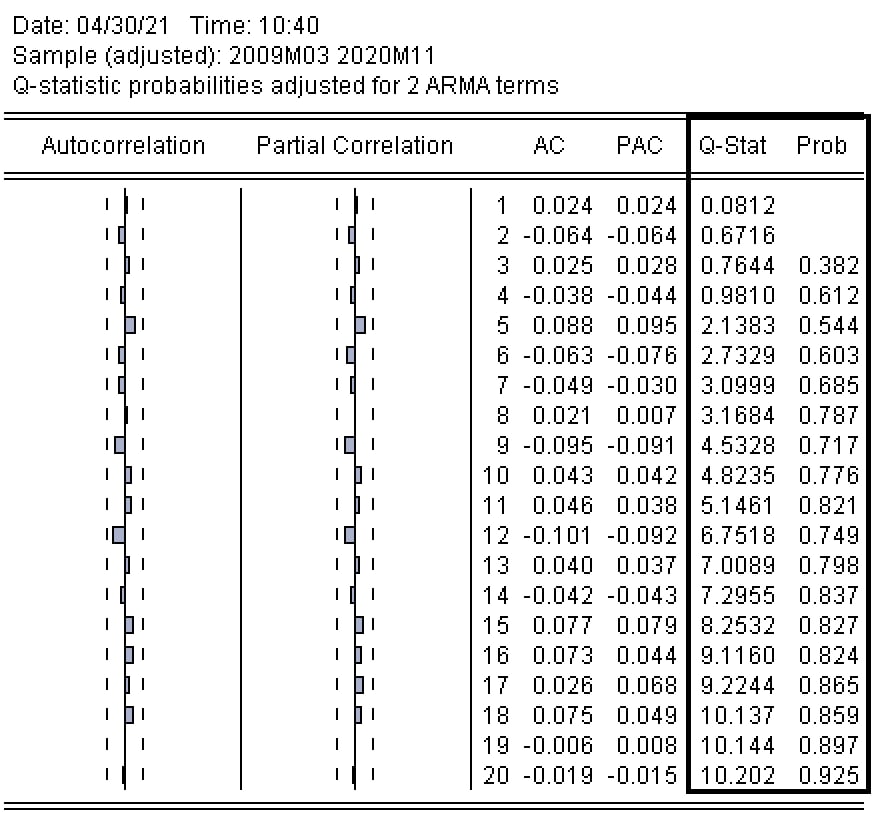
Kiểm tra tự tương quan:
Để kiểm tra tự tương quan, bạn tiến hành quan sát biểu đồ tương quan của mô hình ARIMA (1,1,3) và xem xét thống kê Ljung Box Q, trong đó giả thuyết rỗng là “phần dư là nhiễu trắng”.
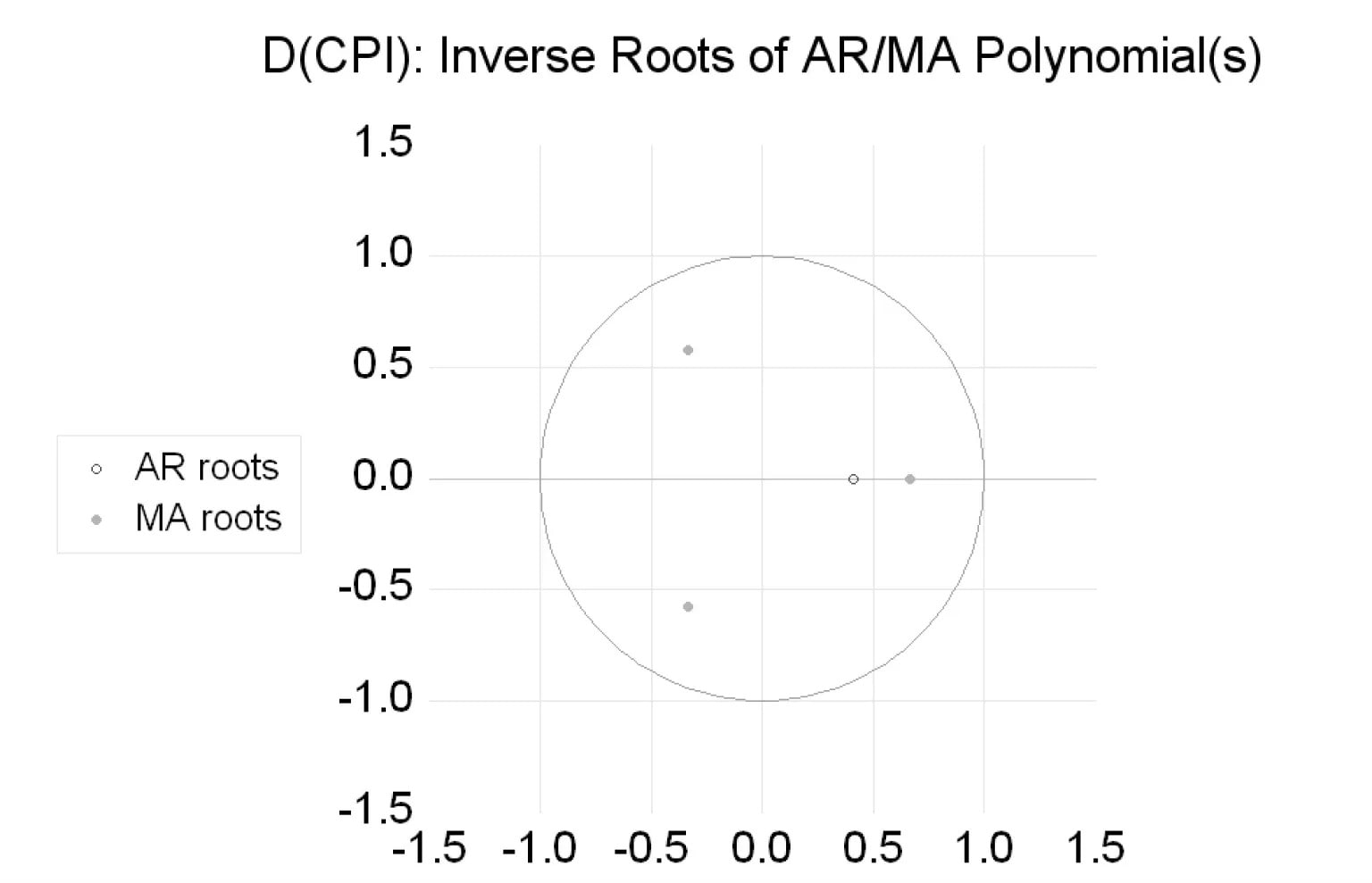
Kiểm tra điều kiện ổn định:
Khi kiểm tra điều kiện ổn định cần đảm bảo 2 yếu tố:
- Mô hình ước tính là hiệp phương sai đứng yên: các gốc AR nghịch đảo phải nằm bên trong vòng tròn đơn vị.
- Quá trình ước tính là không thể đảo ngược: các gốc MA nghịch đảo phải nằm bên trong vòng tròn đơn vị.
Kết quả:
Từ biểu đồ, ta có thể thấy tất cả các gốc nghịch đảo đều nằm bên trong vòng tròn đơn vị.
=> ARIMA (1,1,3) đáp ứng các điều kiện ổn định và điều khoản lỗi là tiếng ồn trắng.
Lưu ý:
Nếu mô hình đã chọn không thỏa mãn điều kiện ổn định, bạn cần phải lặp lại giai đoạn 2 và 3 một lần nữa, đồng thời tìm một ứng viên khác để kiểm tra.
4.4. Giai đoạn dự báo bằng mô hình ARIMA
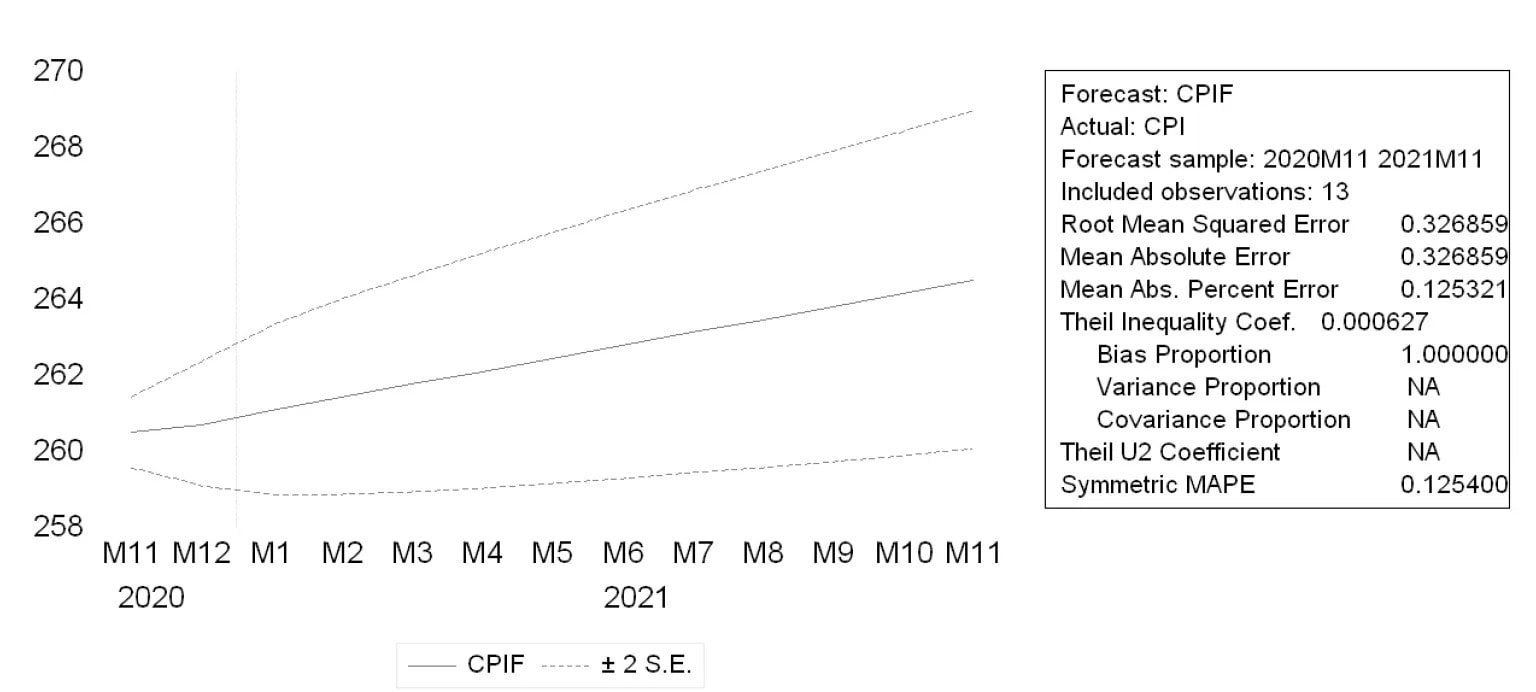
Sau khi kiểm định mô hình bằng chẩn đoán, bạn tiến hành dự báo đơn vị thời gian tiếp theo bằng mô hình ARIMA.
Dự báo ARIMA (1,1,3) – CPI:
- Dự báo bằng cách chạy mô hình ARIMA trên Eviews: Bạn Bấm vào chức năng Forecasting trong bảng Equation.
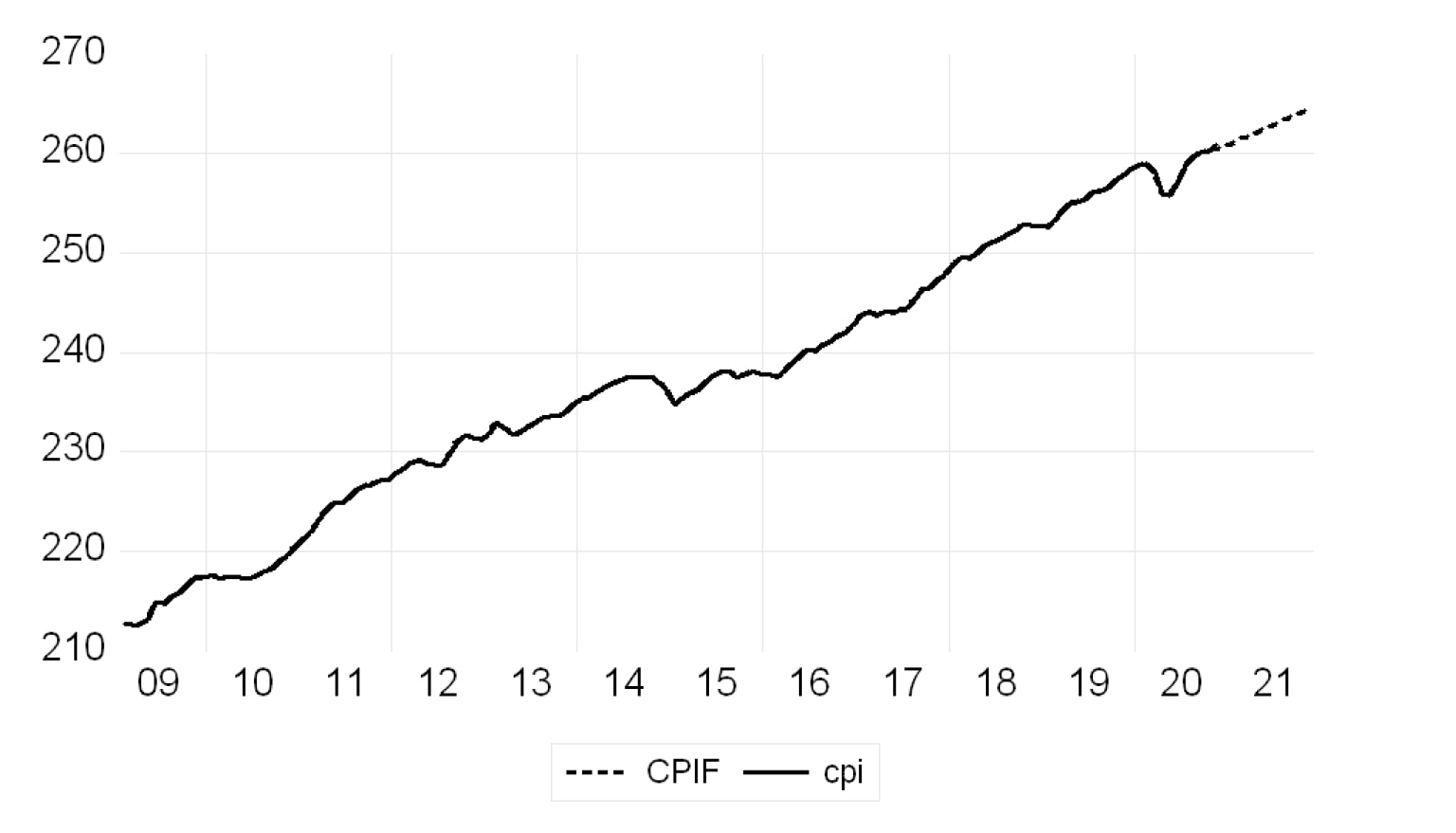
- Vẽ sơ đồ chuỗi gốc và các giá trị dự báo cùng nhau:
Kết luận:
Khẳng định rằng phần dư có phân phối chuẩn.
Vậy là Best4Team vừa chia sẻ đến bạn đọc cách chạy mô hình ARIMA trên Eviews chuẩn xác nhất hiện nay qua 4 giai đoạn chi tiết. Chúng tôi hy vọng rằng qua bài viết này bạn đã nắm vững những thông tin cũng như cách chạy ARIMA trên phần mềm Eviews để ứng dụng vào thực tiễn khi thực hiện nghiên cứu kinh tế lượng. Chúc bạn đọc thành công!